O problema de dobrar uma folha de papel n vezes já é bem conhecido entre os matemáticos. O experimento consistente simplesmente em utilizar uma folha em branco (de preferência uma folha "A4"), e ir unindo seus vértices, de modo que cada dobra reduza a área da folha pela metade. É evidente que, a cada novo movimento, a folha fica cada vez menor e, consequentemente, sua espessura vai aumentando cada vez mais. Você pode tentar reproduzir essa experiência em casa, porém, antes de prosseguir, tente responder: quantas vezes você acha que pode dobrar a folha? Se você executar essa experiência, verá que só é possível dobrar a folha s7 ou 8 vezes, no máximo.
Mesmo que seja extremamente difícil dobrar o papel 8 vezes, não é impossível ir além disso. Em 2002, a norte-americana Britney Gallivan conseguiu dobrar uma folha 12 vezes, estabelecendo um recorde mundial. Se não fosse o bastante, ela ainda deduziu uma fórmula que nos permite determinar o número de dobras que é possível fazer em um material, levando em conta sua espessura, composição etc. A fórmula de Gallivan é:
Para determinar isso, é necessário que o leitor perceba que, ao dobrar a folha uma vez (n=1), a espessura "e" da folha aumenta duas vezes de tamanho. Se você dobrar a folha novamente (n=2), a espessura da folha passa a ser 4 vezes o valor inicial. Se você dobrar uma terceira vez, a espessura passa a ser 8 vezes maior, e assim por diante. Diante disto, é evidente que temos um caso de um crescimento exponencial simples, que pode ser representado por e=2^n , onde "e" é a espessura e n é o número de dobras do papel. No entanto, para sabermos qual o tamanho do papel após um número n de dobras, precisamos multiplicar essa expressão pela espessura inicial do papel, e uma folha "A4" típica tem uma espessura média de 0,1 mm. Sendo assim, obtemos nossa expressão matemática para calcular o tamanho final do papel:
Essa é, de fato, uma fórmula bem simples, mas os resultados que podemos obter com ela são difíceis de assimilar, e nos mostram o quão rápido se dá um crescimento exponencial (ou decrescimento). Pois bem, vamos pôr a "mão na massa" e ver alguns resultados impressionantes (e inacreditáveis).
1- Com 17 dobras, a espessura do papel ficará com cerca de 1,8 metros, praticamente a altura média de um homem adulto;
2- Com apenas 36 dobras, a espessura chegaria aos 400 km, que é praticamente a distância em que a ISS (Estação Espacial Internacional) se encontra da Terra.
3- Com apenas 45 dobras, a espessura atinge um valor de cerca de 385000 km, que é a distância entre a Terra e a Lua;
4- Achou esse resultado impressionante? Bem...saiba que, com apenas 107 dobras, o papel ficaria com uma espessura equivalente ao raio do Universo observável, que é de cerca de 92 bilhões de anos-luz!
Esse realmente é um resultado incrivelmente impressionante, mas antes que você "quebre" a cabeça com isso, é importante frisar que é óbvio que esse experimento é fisicamente impossível de ser executado. Sem entrar em discussão nas questões óbvias, observe que a medida que o papel é dobrado, sua base (a área de um retângulo é o produto da base pela altura) vai diminuindo cada vez mais, de modo que quanto maior fosse a espessura, menor seria a largura da base, e obviamente existe um limite pra tudo isso.
Como mencionado acima, esse "experimento mental" é um ótimo exercício que nos mostra o quão rapidamente ocorrem as mudanças de natureza exponencial, e o fato é que muitos fenômenos físicos obedecem a algumas dessas regras, como é o caso do decaimento radioativo, por exemplo. A análise físico-matemática das coisas nos mostra realmente como é a natureza, e no quão maravilhoso e complexo é o seu comportamento.
Links Úteis
- https://www.guinnessworldrecords.com/world-records/494571-most-times-to-fold-a-piece-of-paper
- https://universoracionalista.org/um-papel-dobrado-ao-meio-107-vezes-fica-maior-do-que-o-universo/
- https://www.youtube.com/watch?v=x24Ns0Q7dh8

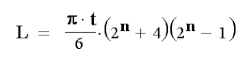

Pois é, tô aqui fazendo o teste pra ter certeza, não sou muito bom com fórmulas.
ResponderExcluirÉ isso aí, Geovane.
Excluir