Como determinar o ponto em que duas retas se intersectam?

Duas retas concorrentes são aquelas que possuem um único ponto em comum. Para determinar o ponto em que duas retas $r$ e $s$ se encontram, basta solucionar o sistema linear de equações formado pelas equações das referidas retas. A equação que descreve uma reta, em sua forma geral, pode ser escrita da seguinte forma: $$ax + by + c = 0$$ onde $a$, $b$ e $c$ são constantes.

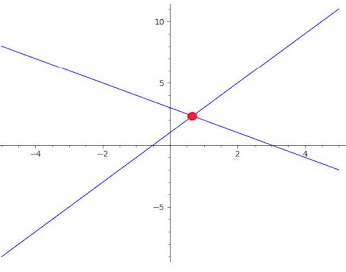
Para vermos isso na prática, considere duas retas, $r$ e $s$, e suas respectivas equações, $r: x - y +1 = 0$ e $s: 2x + y - 2 = 0$. Somando essas duas equações, obtemos: $$3x - 1 = 0$$ que resulta em $x = 1/3$. Para descobrirmos o valor de $y$, basta substituirmos $x$ em alguma das duas equações apresentadas acima, ou seja, $$2\left (\frac{1}{3} \right) + y - 2 = 0$$ que resulta em $y = 4/3$. Logo, o ponto onde a reta $r$ intercepta a reta $s$ é $\left (\frac{1}{3}, \frac{4}{3} \right)$.

A equação de uma reta ainda pode ser escrita em sua forma reduzida e segmentária, mas esses são assuntos que serão abordados em postagens futuras.

Referências

- https://www.todamateria.com.br/equacao-da-reta/

-https://www.obaricentrodamente.com/2022/12/como-determinar-a-inteseccao-de-duas-retas.html

Comentários

Postagens mais visitadas deste blog

O lado oculto da Lua

Você muito provavelmente já deve ter ouvido falar no "lado oculto da Lua", ou, mais especificamente, no "lado escuro da Lua". A cultura popularizou esse termo através de filmes, histórias, canções (como o famoso álbum de 1973 de Pink Floyd), no entanto, não é correto falar em lado escuro da Lua, pois ambos os lados são iluminados pela luz do Sol. O que acontece, de fato, é que a Lua possui um lado que não conseguimos ver; repare que, ao longo do mês, sempre vemos a Lua com um mesmo aspecto visual, e isso pode ser melhor visualizado na figura abaixo. A foto da esquerda é a face da Lua que podemos observar. Perceba que a principal diferença entre ambas as faces é o fato de que o lado oculto (foto da direita) possui uma quantidade bem menor das imensas manchas escuras que o lado visível possui, que nada mais são do que registros do passado geologicamente ativo do nosso satélite. No entanto, a dúvida que fica é: se a Lua gira em torno de si mesma, porque vemos apenas ...

Encontrando a equação da reta tangente à uma curva num ponto $x_0$

Uma aplicação muito interessante sobre derivadas nos permite encontrar, de forma bastante simples, a equação da reta tangente à uma curva num dado ponto $(x_0,y_0)$. Neste texto, irei mostrar de forma muito simples como podemos encontrar a equação tangente à uma curva qualquer num certo ponto $x_0$. Observe o gráfico abaixo. Fonte: respondeai.com.br/calculo O gráfico acima apresenta uma curva $f(x)$ e uma reta que tangencia essa curva no ponto $P$, que possui coordenadas $(x_0,y_0)$. Do cálculo diferencial e integral, sabemos que a inclinação da reta tangente com relação ao eixo $x$ representa a derivada de $f(x)$ com relação a variável $x$. A inclinação $m(x_0)$ da reta pode ser calculada por $$m = \frac{∆y}{∆x}=\frac{y-y_0}{x-x_0}$$ e, como a inclinação representa justamente a derivada, concluímos que $m(x_0) = f'(x_0)$ no pont...

Função par e função ímpar

As funções matemáticas podem apresentar uma variedade muito grande de propriedades. Uma propriedade que é muito interessante é chamada de "paridade", que classifica as funções como sendo par ou ímpar. A paridade de uma função nos ajuda a determinar como será o comportamento gráfico dessa função para determinados valores de $x$, pois funções pares exibem uma simetria com relação ao eixo $y$, enquanto funções ímpares possuem uma simetria com relação à origem do sistema cartesiano. Vejamos isso em mais detalhes nos tópicos abaixo. Função par Uma função $f(x)$ é dita "par" se, e somente se, $f(x) = f(-x)$ para todo $x$ referente ao domínio da função. Ou seja, se substituirmos $x$ em $f(x)$ por $-x$, obtemos o mesmo resultado ou imagem, daí resulta o fato da simetria. Perceba, na imagem acima, que as áreas embaixo das retas (lado esquerdo e direito) são exatamente iguais; é como se a figura da esquerda fosse a parte refletida da figura da direita (e vice-versa). Em cálcu...

FilosoFísica

Pesquisar este blog