Os Primórdios da Física Quântica

1. Introdução

A história da física quântica começa a partir do anseio dos físicos em explicar alguns fenômenos que não encontravam explicação quando analisados à luz dos modelos clássicos. O problema da radiação do corpo negro e o efeito fotoelétrico, em especifico, são tais fenômenos que serviram de ponto de partida para essa nova área emergente da física.

A diferença fundamental, pelo menos sob uma perspectiva conceitual, entre física clássica e física quântica, é que ambas direcionam seu arcabouço teórico e prático à descrição de fenômenos que operam em escalas diferentes de tempo e espaço. A física clássica trata do estudo dos fenômenos que ocorrem em escala macroscópica, isto é, os fenômenos cujas ocorrências são palpáveis a percepção humana. Já a física quântica trata do estudo de fenômenos que ocorrem em escala microscópica, e seus objetos de estudo são moléculas, átomos, partículas, subpartículas, campos etc.

Mesmo que uma teoria estude objetos muito pequenos (comparados aos da física clássica), não seria absurdo imaginar que a descrição que fosse válida para uma, também o valesse para a outra, afinal, em física quântica se emprega os mesmos conceitos de energia, momento, velocidade, posição etc., que são pertinentes na física clássica. Entretanto, a descrição fornecida pela mecânica quântica acerca de várias grandezas físicas só pode ser feita de forma estatística. Sendo assim, ao invés de dizer que um elétron, por exemplo, pode ser encontrado numa dada posição x em um instante de tempo t qualquer, diz-se que existe uma chance desse elétron ser encontrado nessa posição x.

O tratamento estatístico empregado na descrição de um sistema quântico advém do fato de que, diferentemente do que apregoa a física clássica, as partículas não são mais apenas encaradas como massas pontuais se deslocando de um ponto a outro do espaço, mas também apresentam caraterísticas de ondas! Esse aspecto peculiar é conhecido como dualidade onda-partícula. Diferentemente de uma partícula, uma onda não possui uma posição bem definida no espaço porque ondas se estendem ao longo deste, e isto enseja a necessidade de uma nova maneira de se reportar aos fenômenos microscópicos, pois a física clássica encontrou uma imensa limitação em dar conta de explicar e descrever estes fenômenos. Outra razão para essa descrição estatística, como é evidente, é que a mecânica quântica lida com sistemas que podem ser constituídos por um número muito grande de elementos, já que a teoria lida com o comportamento de átomos, moléculas, elétrons etc (lembre-se que a ordem de grandeza de um átomo é de 10^-9 m!).

Apesar de a natureza se comportar de maneira esdrúxula em escalas tão diminutas, a mesma não exibe tais comportamentos simultaneamente: ao se fazer uma medida (da posição de uma partícula, por exemplo), apenas um comportamento será observado, ou o de partícula, ou o de onda, mas nunca ambos simultaneamente! Para se livrar das ambiguidades que naturalmente poderiam surgir (afinal, no cotidiano não se vê um objeto como uma cadeira, por exemplo, ser e não ser uma cadeira!), Niels Bohr criou o conceito de complementaridade, cujo objetivo é fornecer uma maior robustez logica nas descrições quânticas, de modo que as explicações referentes a dualidade exibida pela matéria e radiação seja complementar, no sentido de fornecer uma descrição completa do fenômeno, e não oposta. Bohr também criou o seu princípio de correspondência, que visa estabelecer uma relação causal entre os fenômenos quânticos e clássicos, de modo que estes últimos venham a ser apenas um caso particular do primeiro.   

As descrições e prescrições (lembre-se, a física clássica é essencialmente determinística), classicamente, são feitas com o conhecimento das posições e velocidades das partículas que compõem um sistema, e é dessa maneira que se caracteriza o estado de um sistema considerado (aqui, para efeito de simplicidade, entenda o conceito de estado como sendo “situação”). Embora simples, esse ponto de partida básico da ciência física encontrou uma imensa limitação na mecânica quântica com o advento do "princípio da incerteza de Heisenberg, que afirma que “não é possível medir, simultaneamente, a posição e a quantidade de movimento de uma partícula com precisão ilimitada”. Em outras palavras, é possível afirmar que, na escala atômica, não existe o conceito de trajetória!

Esse tratamento estatístico inerente ao comportamento dos sistemas quânticos fez (e faz) com que a física quântica seja sobejamente mal interpretada, de modo que, mesmo hoje, físicos ainda debatem sobre o real significado dos seus resultados, afinal, a física como corpo de conhecimento têm por objetivo fornecer uma descrição pormenorizada dos acontecimentos físicos, e obviamente o conhecimento adquirido sobre o que ocorre em escala atômica deve ser agregado, dado o seu grande impacto epistemológico e sua notável aplicação prática.

Os parágrafos a seguir irão descrever os principais aspectos teóricos e experimentais associados ao surgimento e desenvolvimento da teoria quântica no início do século XX. 

2. O surgimento da Teoria Quântica

O incrível sucesso descritivo e prescritivo da mecânica Newtoniana levou os físicos do século XIX, dentre eles o eminente Lorde Kelvin, a acreditarem que a física era um corpo de conhecimento completo, ou seja, não haveriam mais descobertas a serem feitas, e a tarefa de um físico ali em diante seria apenas fazer medidas e mensurações cada vez mais acuradas.

Se fosse possível atribuir uma data de nascimento da teoria quântica, esta certamente seria o dia 14 de dezembro de 1900, ano em que Max Planck (1858-1947) publicou seu artigo “Sobre a teoria da Lei de distribuição de energia do espectro normal”, apresentado em uma reunião da sociedade Alemã de física. Em seu artigo, Planck propôs uma solução para um problema que não encontrava resposta quando analisado à luz das teorias clássicas: a radiação do corpo negro. Em física, considera-se um corpo negro como sendo um objeto hipotético que absorve toda a radiação que incide em sua superfície. Na época, os físicos estavam interessados em descrever o modo como a energia emitida por um corpo negro distribuía-se ao longo do espectro e como esta variava com a frequência da radiação.

 

 

                                 Figura 1: Caixa com pequeno orifício.

Na figura 1 é ilustrado o problema em questão: uma caixa possui um pequeno orifício, no qual é atravessado por radiação eletromagnética. Considera-se um objeto assim aproximadamente como um corpo negro pelo fato de que grande parte da radiação incidente é absorvida pelas paredes internas da caixa, e, ao se observar o orifício externamente, percebe-se o seu caráter escurecido, independentemente da cor interna da caixa. No entanto, quando um corpo negro é aquecido, ele passa a exibir uma coloração que depende da temperatura em que se encontra, e isto pode ser medido experimentalmente, como mostra o gráfico 1.

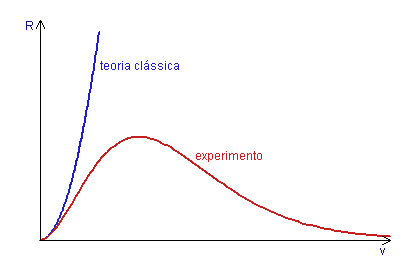
                         Gráfico 1: distribuição espectral da radiação térmica

A grandeza R (eixo vertical) é chamada de "radiança", e a mesma expressa a intensidade da radiação em função da frequência, v. Como pode ser facilmente observado, a curva experimental não corresponde a previsão teórica da teoria clássica. No final do século XIX, Rayleigh e Jeans obtiveram uma expressão que permite calcular a potência irradiada por uma dada cavidade irradiante, mas o seu resultado é fisicamente inaceitável, pois como poder ser observado no gráfico (linha azul), a curva cresce tão rapidamente que tende a infinito. Sendo assim, segundo o modelo de Rayleight-Jeans para um corpo negro, a densidade de energia total irradiada a uma dada temperatura T é infinita! Como foi mencionado acima, esse não é um resultado que fisicamente não pode ser aceito, pois a energia total no universo é finita. Para baixas frequências (pontos próximos à origem dos eixos), observa-se que o modelo de Rayleight-Jeans ainda possui uma concordância com o experimento (sobreposição das linha azul e vermelha), mas a divergência começa a se acentuar na região de frequências próximas do ultravioleta (não está detalhado no gráfico). Por conta disso, essa anomalia passou a ser conhecida como "catástrofe ultravioleta", e representou uma séria limitação da física clássica.

2.1 A hipótese de Planck

A ressureição da hipótese atômica feita pelo químico John Dalton, no início do século XIX, permitiu aos físicos não apenas trabalhar com uma imagem clássica conhecida (tratar os átomos como entidades pontuais massivas), como também fazer uso do que se conhecia por “conceito mecânico’, isto é, a ideia de que se pode utilizar as leis do movimento para descrever o comportamento de uma miríade de sistemas físicos em um tempo arbitrário qualquer. O que se sabia na época, é que se você aquece um determinado material, a uma dada temperatura, este passa a brilhar de forma incandescente, como um filamento de lâmpada.

Ao se utilizar um prisma para decompor os diversos comprimentos de onda que constituem a luz analisada, percebe-se que o mesmo apresenta um espectro contínuo. Os físicos já estavam mais do que convencidos da estreita relação entre a energia radiante emitida por um corpo aquecido e sua temperatura. Neste contexto, a proposta revolucionaria de Planck, contrariando sua própria vontade, era que essa energia radiante não poderia assumir qualquer valor, mas apenas certas quantidades discretas. Mais detalhadamente, “um oscilador de frequência 𝑓 só poderia emitir ou absorver energia em múltiplos inteiros de um quantum de energia”. Matematicamente, isso pode ser escrito como $$E=hf$$onde $E$ representa a energia do oscilador, $f$ é sua frequência e $h$ é a constante de Planck, que é uma das constantes fundamentais na mecânica quântica, cujo valor é $6,63\cdot 10^{-34}$ J.s. A palavra quantum vem do latim e significa “quanto”, de modo que no plural se escreve quanta.

 Esses “osciladores” ao qual Planck se refere diz respeito as próprias partículas que constituem as paredes internas da caixa. Sua proposta é algo totalmente revolucionário e novo na física, pois até em tão não se concebia essa estreita sintonia entre a energia de uma oscilação e sua frequência. Além do mais, os modelos clássicos preveem que a transmissão de energia pode operar com qualquer quantidade, isto é, qualquer valor de energia pode ser absorvido e emitido, como a própria teoria do eletromagnetismo evidencia, uma vez que a energia se propaga na forma de ondas.

 Uma boa analogia para entender a transmissão de energia em forma desses “pacotes”, é imaginar uma transação financeira. Qualquer que seja o valor cedido ou recebido (supondo-se em reais), esta quantidade pode sempre ser expressa como uma combinação, em maior ou em menor número, dos valores disponíveis para a moeda considerada, de modo que o quantum, que é a menor parcela de energia, seria representado por uma moeda de um centavo, que é o menor valor de dinheiro. Sendo assim, uma transferência em dinheiro pode ser feita com o número de centavos que se queira (até mesmo um único centavo), mas jamais poderia ocorrer com uma fração de centavo.

2.2 Efeito Fotoelétrico

A luz sempre despertou um imenso fascínio nos físicos. No século XVII, duas hipóteses diferentes surgiram para tentar explicar a natureza da luz. Uma delas é a hipótese de Newton, em que o mesmo afirmava que a luz era constituída de pequeníssimos corpúsculos materiais. A segunda hipótese, e também a mais acolhida pela comunidade de físicos, foi proposta pelo físico Christian Huygens (1629-1695), ainda no século XVII, de que a luz é uma onda. O fato é que a hipótese de Huygens ganhou imensa aceitação depois dos experimentos de difração realizados por Thomas Young (1773-1829) no século XIX, de modo que todo o desenvolvimento ulterior da teoria eletromagnética foi tecido sob esta premissa.

A teoria eletromagnética desenvolvida por Maxwell atribuía uma natureza eletromagnética para a luz, e isso veio a ser confirmado por Heinrich Hertz (1857-1894), em 1887. Os experimentos conduzidos por Hertz acarretaram na descoberta das ondas eletromagnéticas e do chamado efeito fotoelétrico, que pode ser ilustrado na figura 2 abaixo:

Figura 2: ilustração do efeito fotoelétrico.

O efeito fotoelétrico consiste na emissão de elétrons de uma superfície metálica quando luz incide sobre esta. As as teorias clássicas da física não conseguiam explicar as características desse fenômeno que foram observados, tais como:

1. O efeito era mais facilmente observado quando se utilizava luz de frequências mais elevadas;

2. A taxa de emissão dos elétrons era proporcional a intensidade da luz, diferentemente de sua energia cinética.

Como foi visto anteriormente, a proposta de Planck foi considerar que a matéria absorve e emite energia de forma discreta, mas sua hipótese não havia sido estendida para a energia da radiação. Esse passo foi dado por Albert Einstein (1879-1955), na época um então funcionário do departamento de patentes em Berna, na Suíça. Os elétrons ejetados do metal se deslocam com uma energia cinética que pode ser calculada pela seguinte equação:$$E_c= eV= hf - \Phi$$onde "$e$" representa carga elétrica do elétron, $V$ é a diferença de potencial entre as placas, $h$ é a constante de Planck,  $f$ é a frequência da onda incidente e Ф é chamado de "função trabalho", e representa a energia mínima necessária para "arrancar" os elétrons de superfície do metal. Einstein demonstrou que para cada substância existe uma “frequência de corte”, ou seja, um valor para a frequência da radiação no qual é suficiente para ejetar os elétrons de um determinado material. A grande engenhosidade de Einstein foi ter introduzido o conceito do quantum em sua explicação. Segundo o próprio Einstein: “Se a fórmula deduzida (equação acima) é correta, um gráfico de $V$ em função da frequência da luz incidente, deve resultar numa reta, cujo coeficiente angular deve ser independente da natureza da substancia iluminada”. Devido a este trabalho, e não pela teoria da relatividade, que Einstein fora laureado com o prêmio Nobel de física de 1921.

2.3 Efeito Compton

Uma das mais notáveis contribuições da teoria quântica foi explicar detalhadamente o processo de interação entre matéria e radiação, embora existam certos limites para o que pode ser conhecido e medido, como será visto mais a frente. Mesmo diante de seu sucesso descritivo, o postulado de Einstein, e seus consequentes resultados, não comprovam a existência do fóton. Por sinal, a palavra “fóton”, utilizada para designar um “quantum de luz”, foi batizada por Gilbert Lewis, em 1926.

Um indício fortíssimo acerca da existência dos fótons foi obtido em 1923 por Arthur Holly Compton (1892-1962), quando este observou que o comprimento de onda de um feixe de raios-X espalhados são ligeiramente maiores do que os do feixe incidente. Esse fenômeno de espalhamento é conhecido como efeito Compton. O esquema simplificado é ilustrado na figura 3 abaixo.

                      Figura 3: esquema simplificado do efeito Compton

Utilizando um alvo de grafite, Compton mediu os raios-X espalhados através de um detector e notou que sua intensidade guarda uma relação com o ângulo de espalhamento. Assim como os dois problemas discutidos anteriormente, o efeito Compton encontra uma série de adversidades explicativas quando analisado à luz do eletromagnetismo clássico, que trata a luz como um conjunto de campos elétricos e magnéticos oscilando senoidalmente em função do tempo. Compton (e independentemente Debye) interpretou seus resultados experimentais postulando que o feixe de raios-X incidente não era uma onda de frequência $𝑓$, mas um conjunto de fótons, cada um com energia $ℎ𝑓$, e que esses fótons colidiam com os elétrons livres do alvo da mesma forma que colidem duas bolas de bilhar. Esse argumento é coerente para explicar o fenômeno pois ao abordar o problema (caso ideal simplificado) como uma colisão de partículas, tem-se que o fóton incidente (que compõe os raios-X) transfere parte de sua energia, $ℎ𝑓$, ao elétron, que, por sua vez, é desviado numa dada orientação.

Como uma parte da energia dos fótons incidentes foi transmitida aos elétrons (a energia total permanece inalterada), a energia do feixe espalhado, $ℎ𝑓′$, é menor que a do feixe incidente, $ℎ𝑓$, que implica em $𝑓′<𝑓$, e, por sua vez, $𝜆’ > λ$ (a frequência de uma onda é inversamente proporcional ao seu comprimento de onda, isto é, quanto maior for a frequência, menor o comprimento de onda, e vice-versa). Compton encontrou a seguinte relação que mostra a variação do comprimento de onda da radiação em função do ângulo de espalhamento Ф: $$\Delta\lambda = \lambda' - \lambda = \frac{h}{mc}(1 - \cos\Phi)$$ onde 𝜆′ é o comprimento de onda desviado, 𝜆 é o comprimento de onda inicial, m é a massa do elétron, h é a constante de Planck e c é a velocidade de luz no vácuo. Como foi mencionado no início deste tópico, a explicação dada por Compton para o efeito de deslocamento é exitosa quando se incorpora as ideias de Einstein e Planck. 

2.4 Modelo Atômico de Bohr 

Os fenômenos descritos anteriormente revelam sobejamente a limitação que a física clássica apresenta para explicar tais fenômenos. No entanto, mesmo que a explicação desses fenômenos seja de preponderante importância para o início de uma nova física, o que se apetecia na época, era entender a estabilidade do átomo, e é precisamente neste quesito que a física clássica sofre um “xeque-mate” (dentro do contexto de explicar os fenômenos em escala microscópica).Os dados coletados a partir das experiencias de espalhamento de partículas α obtidos por Ernest Marsden e Hans Geiger levaram Ernest Rutherford (1871-1937) a conclusão de que átomo não só é um todo divisível – como já mostrara J.J. Thomson quando descobriu o elétron em 1897 – como também possui quase toda a sua massa concentrada em seu centro.De uma maneira geral, o que os experimentos de Rutherford mostraram é que a matéria é, em grande parte, espaço vazio.

No modelo5 atômico proposto por Rutherford, o núcleo contém quase toda a massa do átomo e é composto por cargas elétricas positivas, enquanto é rodeado por elétrons que giram ao seu redor em órbitas clássicas. Todavia, como já era sabido desde a época de Maxwell, cargas elétricas aceleradas deviam emitir radiação eletromagnética, e, no modelo de Rutherford, os elétrons são constantemente acelerados pela força de interação de Coulomb que atua como força centrípeta. Essa situação faria com que os elétrons adquirissem um movimento espiralado até atingirem o núcleo, dado que eles constantemente estariam emitindo energia em forma de radiação eletromagnética. Em outras palavras, no modelo atômico de Rutherford, a matéria colapsaria sobre si mesma!

Antes de prosseguir, é importante frisar que o modelo de Bohr ganhou grande aceitação devido ao seu sucesso descritivo acerca do espectro do hidrogênio (figura abaixo), que por sinal, é o átomo no qual o seu modelo tem validade. Ciente acerca das limitações da física clássica para explicar os problemas emergentes, Bohr convenceu-se acerca da utilidade que os postulados de Planck e Einstein teriam para a criação de seu modelo.

                              

             Figura 4: Decomposição da luz emitida por um tubo contendo gás hidrogênio.

A espectroscopia é de sobeja importância para ciências como a química e a astrofísica pois é uma ferramenta poderosa na análise da constituição dos objetos, em especial estrelas, planetas, cometas etc. Bohr fundamentou sua explicação acerca deste fenômeno baseando-se em três postulados:

1. Postulado das órbitas estacionárias: neste postulado, Bohr sugeriu que os elétrons de um átomo podem circular em torno do núcleo em órbitas clássicas sem emitir nenhum tipo de energia na forma de radiação.

2. Postulado da frequência: segundo Bohr, não existem camadas intermediárias entre duas órbitas; os elétrons só ocupam especificamente estas camadas, de modo que cada uma possui uma energia associada. Sendo assim, para um elétron, incialmente numa camada de energia $𝐸1$, ser promovido para uma órbita de energia $𝐸2$, de modo que $𝐸2>𝐸1$, então essa só é possível se este elétron absorver um fóton, e esse fenômeno é conhecido como salto quântico. A energia do fóton é dada pela diferença de energia entre as órbitas: $$E_2 - E_1 = hf = \frac{hc}{\lambda}$$ onde $𝐸2$ é a energia da associada a uma órbita mais energética e $𝐸1$ é a energia associada a uma órbita menos energética.

3. Quantização do momento angular: outra proposta sagaz de Bohr foi quantizar o momento angular, $L$, do elétron: $$L = nℏ$$(onde ℏ é igual a constante de Planck dividido por 2𝜋). Com esses três postulados simples, Bohr foi capaz de deduzir as expressões para as órbitas estacionárias permitidas para os elétrons e suas energias correspondentes. Sendo assim, de acordo com a mecânica clássica, o problema de um elétron orbitando em torno de um próton (figura 6) no átomo de H, sujeito apenas a força de coulombiana, é inteiramente análogo ao problema de Kepler de dois corpos na gravitação, levando a órbitas em geral elípticas, como as dos planetas, podendo haver, como caso particular, órbitas circulares. O modelo atômico proposto por Bohr pode está esquematizado no figura abaixo

                               
                        Figura 5: modelo atômico de Niels Bohr.

A fórmula que Bohr encontrou para a energia de cada órbita pode ser dada por: $$E_n = \frac{-13,6 eV}{n^2}$$

A quantidade n presente na equação acima representa o número quântico associado as órbitas permitidas para os elétrons, que só assumem valores inteiros e é chamado de número quântico principal. A energia da primeira órbita, ou seja, para $n=1$, vale -13,6 𝑒𝑉. Como n não assume valores menores que 1, eventualmente este é o menor nível de energia possível para o átomo de hidrogênio, e esta configuração é conhecida como estado fundamental do hidrogênio. Isso quer dizer que para extrair um elétron que se encontra nesse estado de energia, é necessário fornecer 13,6 𝑒𝑉 de energia a esse elétron.

REFERÊNCIAS BIBLIOGRÁFICAS

ALONSO, M; FINN, E. J. Física: um curso universitário. Coordenador de tradução: Giorgi Moscati. São Paulo: Edgard Blucher, 1972.

BOHR, N.H.D. Física atômica e conhecimento humano: ensaios 1932-1957. 3ª ed. Rio de Janeiro: Contraponto, 1995.

BRENNAN, R. Gigantes da física: uma história da física moderna através de oito biografias. Ed rev. Rio de Janeiro: Jorge Zahar, 2003.

BAKER, J. 50 ideias de Física Quântica que você precisa conhecer. 1ª ed. São Paulo: Planeta, 2015.

CHIBENNI, Silvio Seno. O surgimento da Física Quântica: notas de aula. 2011c. Disponível em:

http://www.unicamp.br/~chibeni/textosdidaticos/fisquantica.pdf. Acesso em 12 de Fevereiro de 2019.

EISBERG, R; RESNICK, R. Física Quântica: átomos, moléculas, sólidos, núcleos e partículas. 35ª ed. Rio de Janeiro: Elsevier, 1979.

FISICA.net. Mecânica Quântica, c2014. Disponível em: http://www.fisica.net/mecanica-quantica/. Acesso em 03 de Março de 2019.

GRIFFITHS, D.J. Mecânica Quântica. Tradução: Lara Freitas. 2ª ed. São Paulo; Pearson, 2011.

HEWITT, P. Física conceitual. 9ª ed. Tradução: Triste Freire Ricci. São Paulo: Bookman, 2008.

NUSSENZVEIG, H.M. Curso de Física Básica: ótica, relatividade e física quântica. 2ª ed. v.4. São Paulo: Blucher, 2014.

OLIVEIRA, I. Física moderna para iniciados, interessados e aficionados. vol.1. 2ª ed. Rio de Janeiro: Livraria da Física, 2005.

PIRES, A.S.T. Evolução das ideias da Física. 2ªed. São Paulo: Livraria da Física, 2011.